浅谈可并堆-启发式合并-左偏树

发表于 | 分类于 ，

普通的二叉堆是一颗完全二叉树，可以支持$O(1)$的查询当前堆内min/max，$O(log n)$的插入和删除节点。他支不支持合并呢？

我们可以首先改变一下堆的写法，把他用一种类似BST(二叉搜索树)的写法写出来，就可以有一种合并的方法！

先用文字描述一下：假设我们要将x和y这两个小根堆合并，我们判断一下如果x的堆顶大于y的堆顶，就交换一下x和y，然后继续合并x的某个子孩子和y。

没看懂上面那一段文字也没关系，我们上图：(图取自教练上课时的课件，应该没关系吧QAQ)


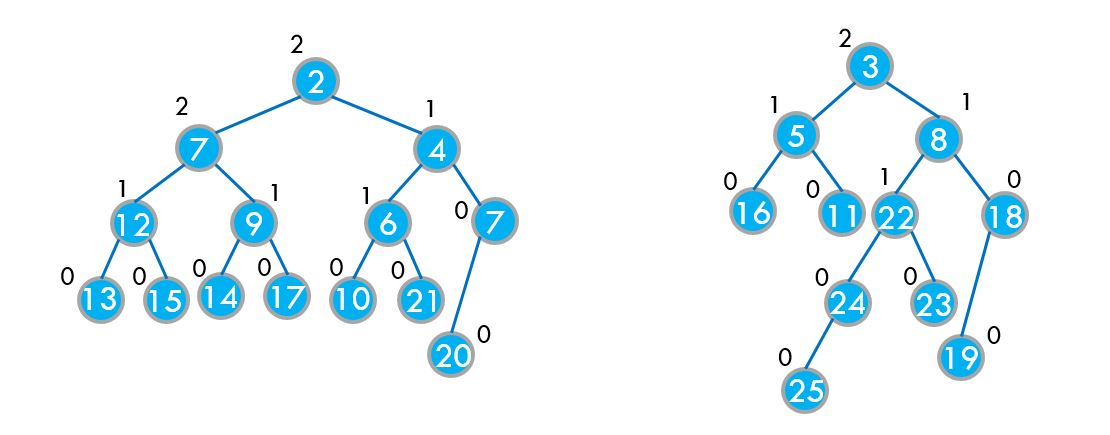
假设我们要合并这两棵树

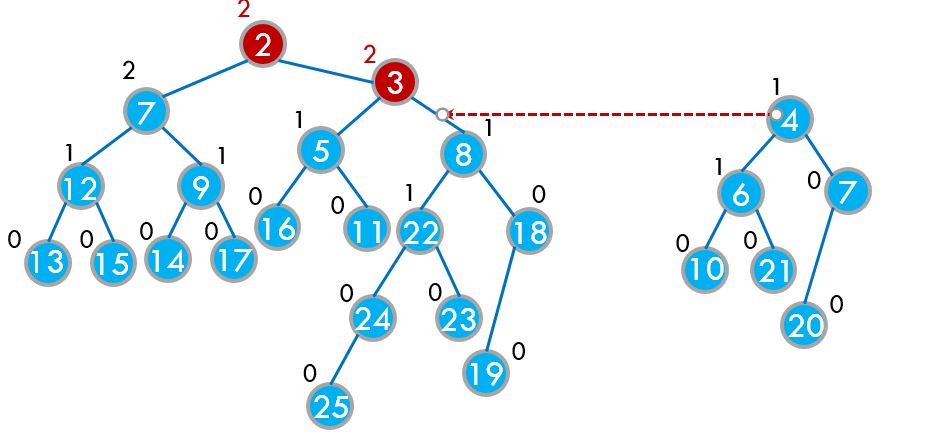
继续往下合并

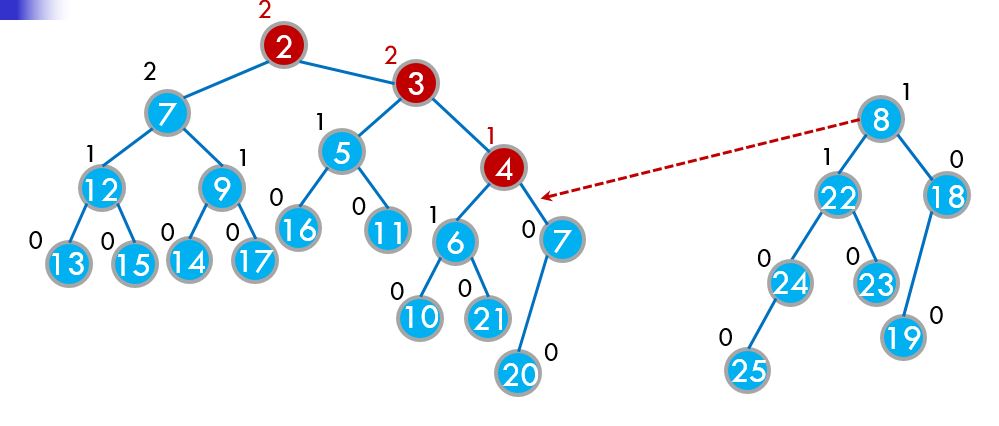
这次合并我们发现x的堆顶大于y的堆顶了，就交换了x和y，然后继续往下合并

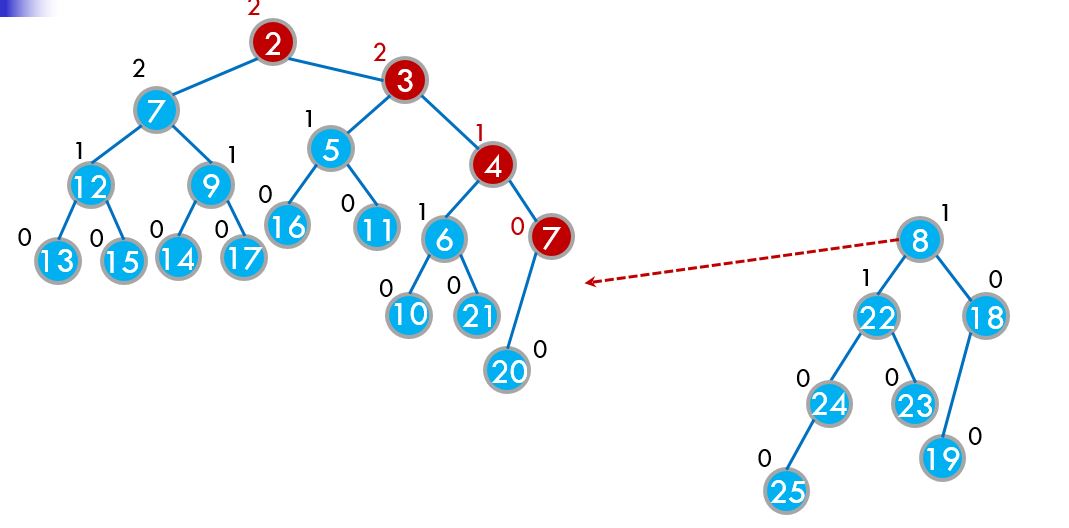
最后我们发现7没有右儿子，就直接让7的右儿子变成y就行了！！

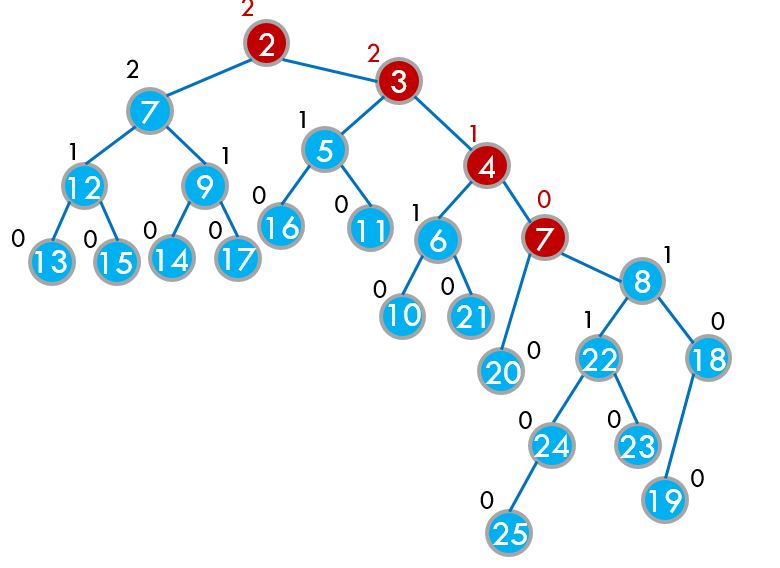
到此，合并正式完成！

但是我们发现这样合并完之后，堆并不再是一颗完全二叉树了，那怎么办呢？

这里就我们可以用一种贪心的思想。其实就是我之前说的继续合并x的某个儿子与y。究竟是哪个儿子呢？

我们这里定义一个值，叫做”根值”，一个节点的根值就是它到最近的叶子节点的距离。其实之前那几张图上每个节点左上角的值就是这个点的根值。

那么我们每次合并就只要合并x的根值最小的儿子和y就行了。这就叫做启发式合并(貌似)。是不是跟并查集的按秩合并有点像啊!

关于他的复杂度，我们可以感性理解为O(两个堆的堆顶的根值)，而用这种启发式合并的话，即使根值最坏也就是$logn$的(完全二叉树)，所以合并一次的复杂度就是$O(log n)$的辣！

那么左偏树又是什么呢？其实就是保证它的右儿子的根值比作儿子小，然后每次合并就只用合并x的右儿子和y就行了！同时回溯的时候发现不满足左偏树性质时就交换左右儿子(感觉没什么用啊)

插入

就是合并一个堆和一个只有一个点的堆。

删除

直接合并它的左右儿子就行了

查询堆顶

直接返回堆顶就行了

关于启发式合并那一块是学了左偏树之后自己YY的，不知道是否叫这个啊？还是有什么别的名字？各位dalao轻喷啊QAQ

下面贴代码吧！指针党福利！(有想看指针版treap的可以去我的题解里)

启发式合并：(通过Luogu P3377,用时405ms)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
#include<iostream>
#define DEBUG printf("PassLine:%d\n", __LINE__)
using namespace std;
const int maxn = 1e5+10; 
struct left_heap{
    int dist, val, idx;
    left_heap *ls, *rs, *fa;
    left_heap(){
        dist = val = idx = 0;
        ls = rs = fa = NULL;
    }
};
int n, m, exist[maxn];
left_heap *tr[maxn];
left_heap *getf(left_heap *x){//找到x所属的堆的根
    while(x->fa != NULL && x!=NULL) x = x->fa;
    return x;
}
left_heap *merge(left_heap *x, left_heap *y){
    if(x == NULL) return y;
    if(y == NULL) return x;
    if(x->val > y->val || (x->val == y->val && x->idx > y->idx)) swap(x, y);//如果x的堆顶的值大于y的堆顶，就交换两个堆
    if(x->ls == NULL) x->ls = merge(x->ls, y);
    else if(x->rs == NULL) x->rs = merge(x->rs, y);
    else if(x->ls->dist < x->rs->dist) x->ls = merge(x->ls, y);//左儿子的根值比右儿子小就继续合并左儿子和y
    else x->rs = merge(x->rs, y);//否则合并右儿子和y
    if(x->ls != NULL) x->ls->fa = x;
    if(x->rs != NULL) x->rs->fa = x;
    if(x->ls == NULL || x->rs == NULL) x->dist = 0;
    else x->dist = min(x->ls->dist, x->rs->dist)+1;//更新x的根值
    return x;
}
int pop(left_heap *x){
    int t = x->val;
    if(x->ls != NULL)x->ls->fa = NULL;
    if(x->rs != NULL)x->rs->fa = NULL;
    if(x->ls != NULL && x->rs != NULL)merge(x->ls, x->rs);//合并左右儿子
    exist[x->idx] = true;
    delete x;//直接在内存中删除x，以防后患+节约内存
    return t;
}
int main(){
    ios::sync_with_stdio(false);
    cin >> n >> m;
    int t;
    for(int i=1; i<=n; i++){
        cin >> t;
        left_heap *la = new left_heap;
        la->val = t; la->idx = i; tr[i] = la;
    }
    int opt, x, y;
    for(int i=1; i<=m; i++){
        cin >> opt;
        if(opt == 1){//合并操作
            cin >> x >> y;
            if(exist[x] || exist[y]) continue;
            if(x == y) continue;
            left_heap *fx = getf(tr[x]), *fy = getf(tr[y]);//找到两个堆的根
            if(fx == fy) continue;
            merge(fx, fy);//合并
        }
        if(opt == 2){
            cin >> x;
            if(exist[x] || exist[getf(tr[x])->idx]){cout << -1 << endl;continue;}
            else cout << pop(getf(tr[x])) << endl;
        }
    }
}

左偏树：(通过Luogu P3377, 用时363ms)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
#include<iostream>
#define DEBUG printf("PassLine:%d\n", __LINE__)
using namespace std;
const int maxn = 1e5+10; 
struct left_heap{
    int dist, val, idx;
    left_heap *ls, *rs, *fa;
    left_heap(){
        dist = val = idx = 0;
        ls = rs = fa = NULL;
    }
};
int n, m, exist[maxn];
left_heap *tr[maxn];
left_heap *getf(left_heap *x){
    while(x->fa != NULL && x!=NULL) x = x->fa;
    return x;
}
left_heap *merge(left_heap *x, left_heap *y){
    if(x == NULL) return y;
    if(y == NULL) return x;
    if(x->val > y->val || (x->val == y->val && x->idx > y->idx)) swap(x, y);
    x->rs = merge(x->rs, y);
    if(x->rs != NULL)x->rs->fa = x;
    if(x->ls == NULL){x->ls = x->rs; x->rs = NULL;}
    else if(x->ls->dist < x->rs->dist) swap(x->ls, x->rs);//主要是这一步，如果左儿子比右儿子根值小，就交换左右儿子
    x->dist = (x->rs == NULL ? 0 : x->rs->dist+1);
    return x;
}
int pop(left_heap *x){
    int t = x->val;
    if(x->ls != NULL)x->ls->fa = NULL;
    if(x->rs != NULL)x->rs->fa = NULL;
    if(x->ls != NULL && x->rs != NULL)merge(x->ls, x->rs);
    exist[x->idx] = true;
    delete x;
    return t;
}
int main(){
    ios::sync_with_stdio(false);
    cin >> n >> m;
    int t;
    for(int i=1; i<=n; i++){
        cin >> t;
        left_heap *la = new left_heap;
        la->val = t; la->idx = i; tr[i] = la;
    }
    int opt, x, y;
    for(int i=1; i<=m; i++){
        cin >> opt;
        if(opt == 1){
            cin >> x >> y;
            if(exist[x] || exist[y]) continue;
            if(x == y) continue;
            left_heap *fx = getf(tr[x]), *fy = getf(tr[y]);
            if(fx == fy) continue;
            merge(fx, fy);
        }
        if(opt == 2){
            cin >> x;
            if(exist[x] || exist[getf(tr[x])->idx]){cout << -1 << endl;continue;}
            else cout << pop(getf(tr[x])) << endl;
        }
    }
}

最后说几句，可并堆还有好几种，如配对堆，斐波那契堆等等，大家想学的可以去看一看！